1. Read the lecture (displayed below) [30-60 minutes]
2. Watch the video    [31:12 minutes]
3. Do the exercises  [~30 minutes]

Total time = [~2:00 hours]

Last Lecture:
In lecture II.1, we carried out the Transmission Line Circuit Analysis Using the Distributed RLCG Model.

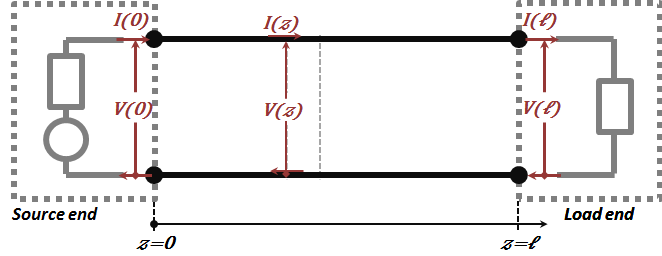
Figure 2.6

The steady-state harmonic analysis in the frequency domain yielded the following expressions for voltage and current expressions:

The corresponding time domain expressions are:

Also, we concluded that the expressions for case of lossless TL $({{R}_{z}}=0~and~{{G}_{z}}=0)$

In lecture II.2, we explored the Physical Implications of Solutions - $\alpha$, $\beta$, λ, and ${{c}_{ph}}$ to conclude that the solution (2.18 – 2.29) represent two waves traveling in opposites sides. The (+) wave and (-) wave travel in both $(+z)$ and $(-z)$ directions, respectively.

Figure 2.9

While in the lossless TL case, the waves on the TL would not suffer any attenuation. The corresponding wave shapes are shown in Figure 2.10.

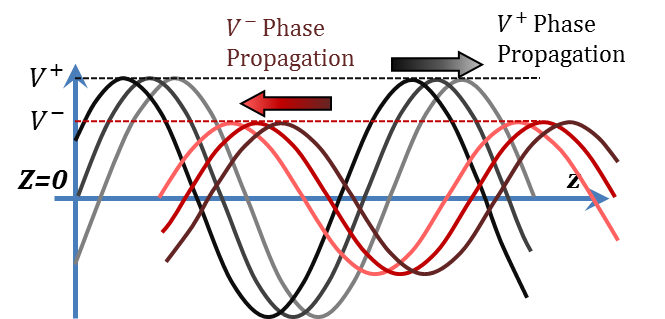
Figure 2.10

Physical Implications of Solutions - $\mathbf{\Gamma }$:

In this lecture, we will learn about the physical implications of the reflection coefficient $Γ(z)$ defined as the ratio between the $–z$ and $+z$ waves. We will also learn about the driving point impedance $Z(z)$ and its relationship to $Γ(z)$.

As per our earlier discussion, the ${{V}^{-}}$ wave results from reflections of the ${{V}^{+}}$ wave as it bounces off the TL "discontinuity" at the load end. Hence, we define the ratio of the "reflected" $(-z)$ wave to the "incident" $(+z)$ wave as the reflection coefficient.

Figure 2.12

From Equation (2.49), we conclude that if it was not for the mismatch ${{Z}_{L}}-{{Z}_{o}}$ between the load impedance $Z_{L}$ and the TL characteristic impedance $Z_{o}$, and as a consequence the reflection coefficient $\text{ }\!\!\Gamma\!\!\text{ }\left( z \right)$, the reflection ($-z$ wave) ${{V}^{-}}{{e}^{+~\gamma ~z}}$ would not exist. Therefore, we can say that waves traveling on a uniform TL with a matched end are fully absorbed by the load and will never experience any reflections. Likewise, if the TL is uniform and infinite in length, with no discontinuities, the source end launched waves would continue to travel indefinitely resulting in the absence of reflections ($-z$ waves). This is exactly what happens to a light beam projected in the open space. If it meets a reflective object (mismatched impedance), a reflection takes place. However, no reflections occur in one of two possible cases, the case of a fully absorbing object (matched impedance) and the case of open space with no intercepting objects.

Before we leave this section, let us finalize the expressions for the voltages and currents at any $z$-location on the line as well as at both the sending and receiving ends: We start by rewriting Equation (2.41) in terms of the $Γ's$ (reflection coefficients) associated with the source and load impedances,

${{\Gamma }_{L}}=\Gamma \left( \ell \right)=~\frac{\left[ {{Z}_{L}}-{{Z}_{o}} \right]}{\left[ {{Z}_{L}}+{{Z}_{o}} \right]}\tag{2.52}$

${{\Gamma }_{s}}=\frac{\left[ {{Z}_{s}}-{{Z}_{o}} \right]}{\left[ {{Z}_{s}}+{{Z}_{o}} \right]}\tag{2.53}$

Note that $Γ_{s}$ is different from $Γ(0)$. $Γ_{s}$ is defined in Equation (2.53) as the reflection coefficient seen by the $"–z"$ signal traveling back towards the source with the source impedance acting as the load to the $Z_{o}$ line. On the other hand $Γ(0)$ is the reflection coefficient seen at the input port of the line by the $"+z"$ wave, $Γ(z=0)=V^{-}/V^{+}$, Equation (2.50).

Now, back to Equation (2.41),

${{\text{V}}^{+}}=\left\{ \frac{{{\text{V}}_{\text{s}}}~\cdot ~{{\text{Z}}_{\text{o}}}}{{{\text{Z}}_{\text{s}}}+{{\text{Z}}_{\text{o}}}} \right\}\left\{ \frac{1}{1-\left( \frac{{{\text{Z}}_{\text{s}}}-{{\text{Z}}_{\text{o}}}}{{{\text{Z}}_{\text{s}}}+{{\text{Z}}_{\text{o}}}} \right)\left( \frac{{{\text{Z}}_{\text{L}}}-{{\text{Z}}_{\text{o}}}}{{{\text{Z}}_{\text{L}}}+{{\text{Z}}_{\text{o}}}} \right){{\text{e}}^{-2\text{ }\gamma\text{ }\ell }}} \right\}=\left\{ \frac{{{\text{V}}_{\text{s}}}~\cdot ~\left[ 1~-{{\text{ }\Gamma\text{ }}_{\text{s}}} \right]}{2} \right\}\left\{ \frac{1}{1~-~{{\text{ }\Gamma\text{ }}_{\text{s}}}~{{\text{ }\Gamma\text{ }}_{\text{L}}}~~{{\text{e}}^{-2\text{ }\gamma\text{ }\ell }}} \right\}=\left\{ \frac{{{\text{V}}_{\text{s}}}~}{2} \right\}\left\{ \frac{1~-{{\text{ }\Gamma\text{ }}_{\text{s}}}}{1~-~{{\text{ }\Gamma\text{ }}_{\text{s}}}~{{\text{ }\Gamma\text{ }}_{\text{L}}}~~{{\text{e}}^{-2\text{ }\gamma\text{ }\ell }}} \right\}\tag{2.54}$

${{\text{V}}^{-}}={{\text{V}}^{+}}\left( \frac{{{\text{Z}}_{\text{L}}}-{{\text{Z}}_{\text{o}}}}{{{\text{Z}}_{\text{L}}}+{{\text{Z}}_{\text{o}}}} \right){{\text{e}}^{-2\text{ }\gamma\text{ }\ell }}=\left\{ \frac{{{\text{V}}_{\text{s}}}~}{2} \right\}\left\{ \frac{1~-{{\text{ }\Gamma\text{ }}_{\text{s}}}}{1~-~{{\text{ }\Gamma\text{ }}_{\text{s}}}~{{\text{ }\Gamma\text{ }}_{\text{L}}}~~{{\text{e}}^{-2\text{ }\gamma\text{ }\ell }}} \right\}\left( \frac{{{\text{Z}}_{\text{L}}}-{{\text{Z}}_{\text{o}}}}{{{\text{Z}}_{\text{L}}}+{{\text{Z}}_{\text{o}}}} \right){{\text{e}}^{-2\text{ }\gamma\text{ }\ell }}=\left\{ \frac{{{\text{V}}_{\text{s}}}~}{2} \right\}\left\{ \frac{\left( 1~-{{\text{ }\Gamma\text{ }}_{\text{s}}} \right)~{{\text{ }\Gamma\text{ }}_{\text{L}}}~~{{\text{e}}^{-2\text{ }\gamma\text{ }\ell }}}{1~-~{{\text{ }\Gamma\text{ }}_{\text{s}}}~{{\text{ }\Gamma\text{ }}_{\text{L}}}~~{{\text{e}}^{-2\text{ }\gamma\text{ }\ell }}} \right\}\tag{2.55}$

Using Equations (2.44), (2.51), and (2.54), we can write the voltage as a function of position as follows:

$\text{V}\left( z \right)={{\text{V}}^{+}}{{\text{e}}^{-\text{ }\gamma z}}\left[ 1+\text{ }\!\!\Gamma\!\!\text{ }\left( z \right) \right]=\left\{ \frac{{{\text{V}}_{\text{s}}}~}{2} \right\}\left\{ \frac{1~-{{\text{ }\Gamma\text{ }}_{\text{s}}}}{1~-~{{\text{ }\Gamma\text{ }}_{\text{s}}}~{{\text{ }\Gamma\text{ }}_{\text{L}}}~~{{\text{e}}^{-2\text{ }\gamma\text{ }\ell }}} \right\}{{\text{e}}^{-\text{ }\gamma z}}\left[ 1+{{\text{ }\Gamma\text{ }}_{\text{L}}}~~{{\text{e}}^{+2\text{ }\gamma\text{ }\left( z-\ell \right)}} \right]$

$\text{V}\left( z \right)=\left\{ \frac{{{\text{V}}_{\text{s}}}~}{2} \right\}\left\{ \frac{\left( 1~~-~{{\text{ }\Gamma\text{ }}_{\text{s}}} \right)\left[ 1~+~{{\text{ }\Gamma\text{ }}_{\text{L}}}~~{{\text{e}}^{+2\text{ }\gamma\text{ }\left( \text{z}-\ell \right)}} \right]}{1~-~{{\text{ }\Gamma\text{ }}_{\text{s}}}~{{\text{ }\Gamma\text{ }}_{\text{L}}}~~{{\text{e}}^{-2\text{ }\gamma\text{ }\ell }}} \right\}{{\text{e}}^{-\text{ }\gamma z}}\tag{2.56}$

Substituting $z=0$ and ${z}=\ell $ in this general expression, we can write the voltages at the sending and receiving ends as,

$\text{V}\left( 0 \right)=\left\{ \frac{{{\text{V}}_{\text{s}}}~}{2} \right\}\left\{ \frac{\left( 1~-{{\text{ }\Gamma\text{ }}_{\text{s}}} \right)\left( 1~+{{\text{ }\Gamma\text{ }}_{\text{L}}}~~{{\text{e}}^{-2\text{ }\gamma\text{ }\ell }} \right)}{1~-~{{\text{ }\Gamma\text{ }}_{\text{s}}}~{{\text{ }\Gamma\text{ }}_{\text{L}}}~~{{\text{e}}^{-2\text{ }\gamma\text{ }\ell }}} \right\}\tag{2.57}$

${{\text{V}}_{\text{L}}}=\text{V}\left( \ell \right)=\left\{ \frac{{{\text{V}}_{\text{s}}}~}{2} \right\}\left\{ \frac{\left( 1~-{{\text{ }\Gamma\text{ }}_{\text{s}}} \right)\left( 1~+{{\text{ }\Gamma\text{ }}_{\text{L}}} \right)~{{\text{e}}^{-\text{ }\gamma\text{ }\ell }}}{1~-~{{\text{ }\Gamma\text{ }}_{\text{s}}}~{{\text{ }\Gamma\text{ }}_{\text{L}}}~~{{\text{e}}^{-2\text{ }\gamma\text{ }\ell }}} \right\}\tag{2.58}$

Alternatively, in terms of impedances, we can write:

$\text{V}\left( 0 \right)={{\text{V}}_{\text{s}}}\left\{ \frac{{{\text{Z}}_{\text{o}}}\left\{ \left( {{\text{Z}}_{\text{L}}}+{{\text{Z}}_{\text{o}}} \right)+~\left( {{\text{Z}}_{\text{L}}}-{{\text{Z}}_{\text{o}}} \right){{\text{e}}^{-2\text{ }\gamma\text{ }\ell }} \right\}}{\left( {{\text{Z}}_{\text{s}}}+{{\text{Z}}_{\text{o}}} \right)\left( {{\text{Z}}_{\text{L}}}+{{\text{Z}}_{\text{o}}} \right)-\left( {{\text{Z}}_{\text{s}}}-{{\text{Z}}_{\text{o}}} \right)\left( {{\text{Z}}_{\text{L}}}-{{\text{Z}}_{\text{o}}} \right){{\text{ e}}^{-2\text{ }\gamma\text{ }\ell }}} \right\}\tag{2.57a}$

${{\text{V}}_{\text{L}}}={{\text{V}}_{\text{s}}}\left\{ \frac{2~~{{\text{Z}}_{\text{L}}}~{{\text{Z}}_{\text{o}}}}{\left( {{\text{Z}}_{\text{s}}}+{{\text{Z}}_{\text{o}}} \right)\left( {{\text{Z}}_{\text{L}}}+{{\text{Z}}_{\text{o}}} \right)-\left( {{\text{Z}}_{\text{s}}}-{{\text{Z}}_{\text{o}}} \right)\left( {{\text{Z}}_{\text{L}}}-{{\text{Z}}_{\text{o}}} \right){{\text{ e}}^{-2\text{ }\gamma\text{ }\ell }}} \right\}{{\text{e}}^{-\text{ }\gamma\text{ }\ell }}\tag{2.58a}$

Two Special Cases: The Infinite Line and the Matched Load Line

Let us assume a TL with infinite length. As we just stated in the previous section, there will be no reflections from the load resulting in $\text{ }\!\!\Gamma\!\!\text{ }\left( \ell \right)=0$, and hence $\text{ }\!\!\Gamma\!\!\text{ }\left({z} \right)=0$ and ${{V}^{-}}=0$.

Consequently, according to (2.18) and (2.23),

$\text{V}\left( {z} \right)={{\text{V}}^{+}}{{\text{e}}^{-\text{ }\gamma { z}}}\text{ }~\text{ and }~\!\!\text{ I}\left( {z} \right)=~\frac{1}{{{\text{Z}}_{\text{o}}}}\cdot \left\{ {{\text{V}}^{+}}{{\text{e}}^{-\text{ }\gamma { z}}} \right\}\tag{2.59}$

which makes $Z\left( z \right)=~{{Z}_{o}}$ at all $z$ locations including $z=0$ (TL input impedance), ${{Z}_{in}}=Z\left( 0 \right)=~{{Z}_{o}}$.

Solving the boundary condition at the source end,

$V\left( 0 \right)={{V}^{+}}={{V}_{s}}-{{Z}_{s}}\cdot I\left( 0 \right)={{V}_{s}}-{{Z}_{s}}\cdot \frac{1}{{{Z}_{o}}}\left( {{V}^{+}} \right)$

which yields:

$\text{V}\left( 0 \right)={{\text{V}}^{+}}={{\text{V}}_{\text{s}}}~\cdot~\frac{{{\text{Z}}_{\text{o}}}}{{{\text{Z}}_{\text{s}}}+{{\text{Z}}_{\text{o}}}}\text{ and}~\text{ I}\left( 0 \right)=\frac{{{\text{V}}^{+}}}{{{\text{Z}}_{\text{o}}}}={{\text{V}}_{\text{s}}}~\cdot~\frac{1}{{{\text{Z}}_{\text{s}}}+{{\text{Z}}_{\text{o}}}}~\tag{2.60}$

Therefore, physically speaking, both an infinite line and a match terminated line exhibit matching at line locations including the line input $(at~z=0)$. Only waves traveling in $+z$ direction can exist on the line.

Standing Waves and Standing Wave Ratio:

The combination of waves traveling in both directions on the same TL is likely to cause standing waves to form. To explain, let us start with the lossless line time- domain combined solution, Equation (2.34). By adding and subtracting the term $\left| {{V}^{-}} \right|\cos \left( \omega t-\beta z+\varphi _{v}^{+} \right)$ in the right hand side of the equation, we obtain:

$v\left( z,t \right)=\left| {{V}^{+}} \right|\cos \left( \omega t-\beta z+\varphi _{v}^{+} \right)+\left| {{V}^{-}} \right|\cos \left( \omega t+\beta z+\varphi _{v}^{-} \right)$

$v\left( z,t \right)=\left\{ \left[ \left| {{V}^{+}} \right|-\left| {{V}^{-}} \right| \right]\cdotp\cos \left( \omega t-\beta z+\varphi _{v}^{+} \right) \right\}+\left\{ \left| {{V}^{-}} \right|\left[ \cos \left( \omega t-\beta z+\varphi _{v}^{+} \right)+\cos \left( \omega t+\beta z+\varphi _{v}^{-} \right) \right] \right\}$

$v\left( z,t \right)=\left\{ \left[ \left| {{V}^{+}} \right|-\left| {{V}^{-}} \right| \right]\cdotp\cos \left( \omega t-\beta z+\varphi _{v}^{+} \right) \right\}+\left\{ 2\left| {{V}^{-}} \right|\left[ cos\left( \omega t+{{\varphi }_{1}} \right)\cdotp\cos \left( \beta z+{{\varphi }_{2}} \right) \right] \right\} \tag{2.61}$

Where ${{\varphi }_{1}}~and~{{\varphi }_{2~}}$ replaces the quantities $\frac{\varphi _{v}^{+}+\varphi _{v}^{-}}{2}$ and $\frac{\varphi _{v}^{+}-\varphi _{v}^{-}}{2}$, respectively.

The first term of the resulting equation, $\left\{ \left[ \left| {{\text{V}}^{+}} \right|-\left| {{\text{V}}^{-}} \right| \right]\cdotp\cos \left( \text{ }\!\!\omega\!\text{ t}-\text{ }\!\!\beta z+\text{ }\!\!\varphi\!\!\text{ }_{v}^{+} \right) \right\}$, has the same traveling form as the positive $z$ traveling wave but with a reduced amplitude of $\left[ \left| {{V}^{+}} \right|-\left| {{V}^{-}} \right| \right]$. On the other hand, the second term, $\left\{ 2\left| {{\text{V}}^{-}} \right|\left[ \cos \left( \text{ }\!\!\omega\!\text{ t}+{{\text{ }\!\!\varphi\!\!\text{ }}_{1}} \right)\cdot \cos \left( \text{ }\!\!\beta z+{{\text{ }\!\!\varphi\!\!\text{ }}_{2}} \right) \right] \right\}$ has an amplitude of $2\left| {{V}^{-}} \right|$ and describes a "standing wave" that does not travel in either direction on the line and t is characterized by stationary "peaks/maxima" and "valleys/minima". This can be seen mathematically by examining the expression and recognizing that the spatial dependence term $\left[ \cos \left( \text{ }\!\!\beta z+{{\text{ }\!\!\varphi\!\!\text{ }}_{2}} \right) \right]$ forces the term to zero at certain $z$ locations irrespective of the time dependent term. This is demonstrated in Figure 2.13.

Figure 2.13

Hence, expression (2.61), as seen in the figure, is a mixture of a traveling wave component and a standing wave one. The amplitude of the standing wave component $2\left| {{V}^{-}} \right|$, is determined by the level of the reflected signal. In the absence of reflections, there will be no standing waves and we get pure traveling waves on the line. However, a $100$% reflection where $\left| {{V}^{-}} \right|=\left| {{V}^{+}} \right|$ results in a pure "$100$%" standing waves on the TL since the traveling wave term $\left[ \left| {{\text{V}}^{+}} \right|-\left| {{\text{V}}^{-}} \right| \right]$ reduces to zero.

Standing Wave Ratio:
An important indicator of the level of standing waves in a TL network is the standing wave ratio, SWR, the definition for which is the ratio of the peak (max) amplitude of the signal and its valley (min) value:

$\text{SWR}=\frac{{{\left| \text{V} \right|}_{\text{max}}}}{{{\left| \text{V} \right|}_{\text{min}}}}=\frac{\left[ \left| {{\text{V}}^{+}} \right|+\left| {{\text{V}}^{-}} \right| \right]}{\left[ \left| {{\text{V}}^{+}} \right|-\left| {{\text{V}}^{-}} \right| \right]}=\frac{1+\left| \text{ }\Gamma\text{ } \right|}{1-\left| \text{ }\Gamma\text{ } \right|}\tag{2.62}$

$\text{SWR}=1$ for a pure traveling waves $(\left| \text{ }\!\Gamma\!\text{ } \right|=0)$ and $\text{SWR}=8$ for a pure standing wave $(\left| \text{ }\!\Gamma\!\text{ } \right|=1)$.

Figure 2.14 is a graphical demonstration of the relationship between the $\text{SWR}$ and $\left| \text{ }\!\Gamma\!\text{ } \right|.$

Figure 2.14

For lossy lines, the line attenuation causes the signals to decay down the TL path, resulting in the signal forms displayed in Figure 2.15.

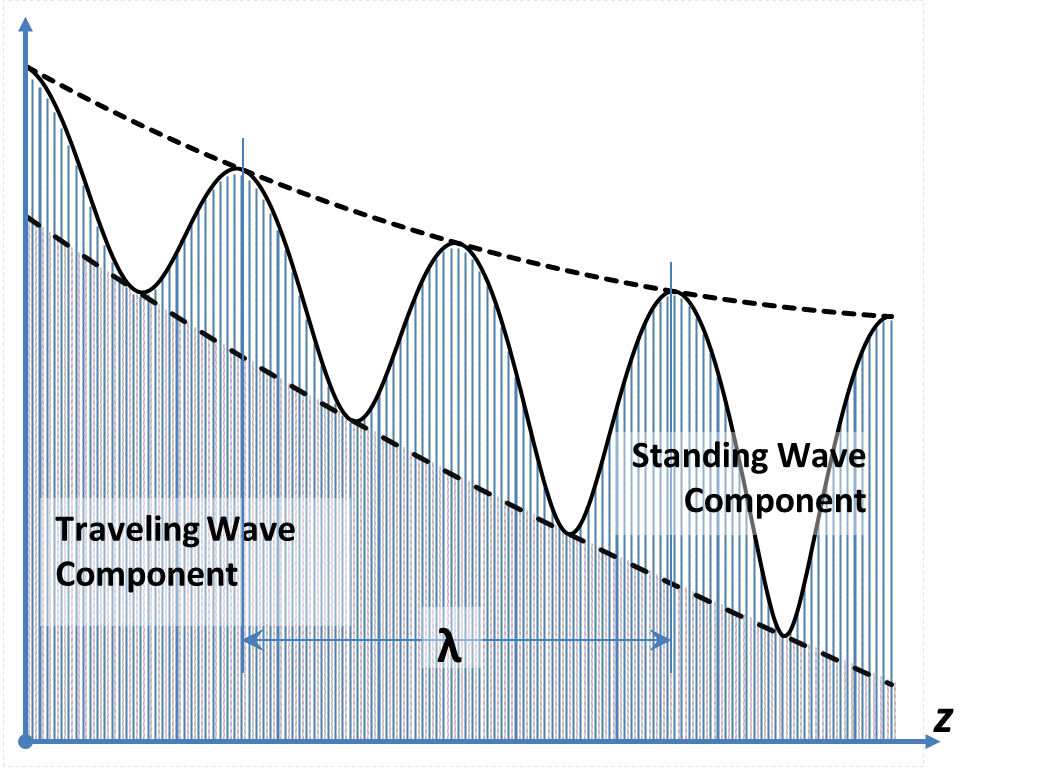
Figure 2.15

The figure shows the presence of a mixture of traveling and standing waves, just as in the lossless case. It is important to note here that since all the levels are changing, it is not possible to define a single value for the $SWR$. It is typical in such cases; to identify the location at which the $SWR$ is given, i.e., the $SWR$ of the load would be that of the nearest minimum and maximum to the TL load.

Another way of looking at the combination of the two traveling waves and their "interference" is to consider the corresponding phasor diagrams. For convenience, we will consider the case of a lossless TL only. In this case, the two phasors representing the two traveling waves are:

${{\text{V}}^{+}}{{\text{e}}^{-j\beta z}}\text{ }\!\!~\text{ and }~\!\!\text{ }{{\text{V}}^{-}}{{\text{e}}^{+j\beta z}}$

Referring to Figure 2.16, we will start with a graph of the two phasors at some location $z_{1}$ where they line up in their phase. As we move from $z_{1}$ to $z_{2}$(where $z_{2}>z_{1})$, the phase of the $V^{+}$ phasor changes by $-\beta \left( {{z}_{2}}-{{z}_{1}} \right)$ (decreases) while the phase of the $V^{-}$ phasor changes by $+\beta \left( {{z}_{2}}-{{z}_{1}} \right)$ (increases). Similarly, we monitor the phasors' rotation as we move to ${{z}_{3}}$ and$~{{z}_{4}}$. The sum of the two phasors is displayed for all four positions in part (b) of the figure, and its magnitude is plotted vs distance in part (c) of the figure. We notice that the sum exhibits the same shape as that demonstrated earlier in Figure 2.13. We also notice that the peaks (maxima) occur when the two phasors line up with equal phases. The spacing between two consecutive peaks correspond to a $180~degrees$ rotation which is equivalent to a distance if λ$/2$.

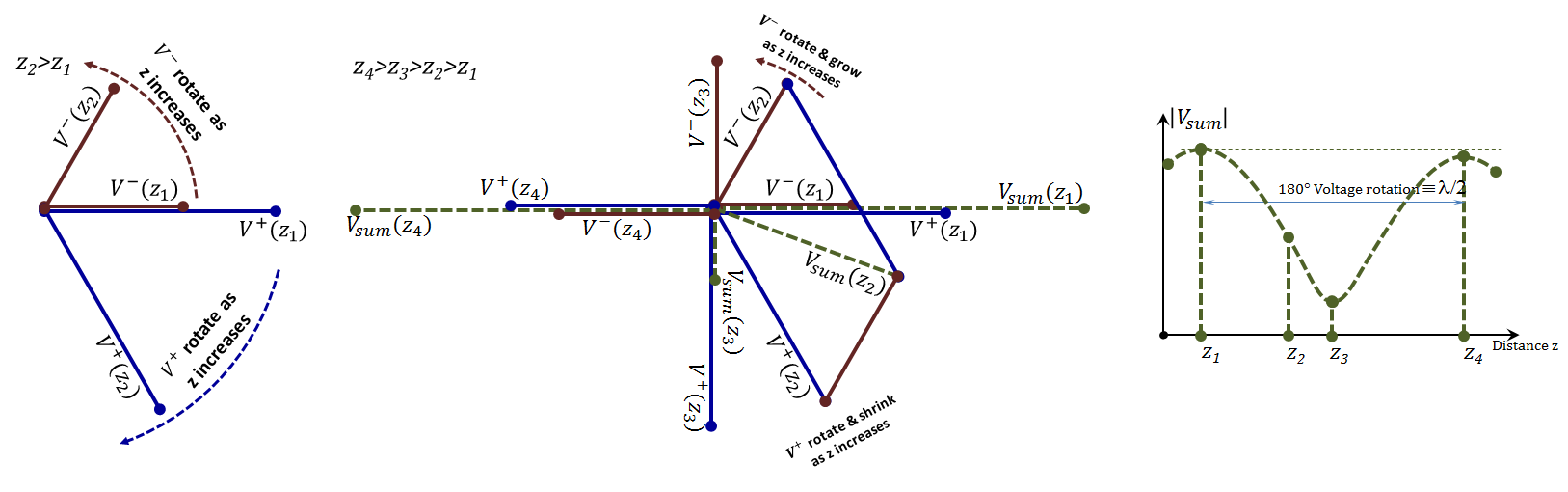
Figure 2.16

Standing Waves and the Bounce Diagram:
In this section, we further our exploration of the physics of the multiple reflections / standing waves in mismatched TL networks. In this regard, we will consider the general case of impedance mismatches at both the source and load ends; hence, we can see that multiple wave reflections will occur on the line with waves bouncing back and forth between the (generally) mismatched TL ends. Figure 2.17 depicts the TL network and the expected "bounce" diagram as a result.

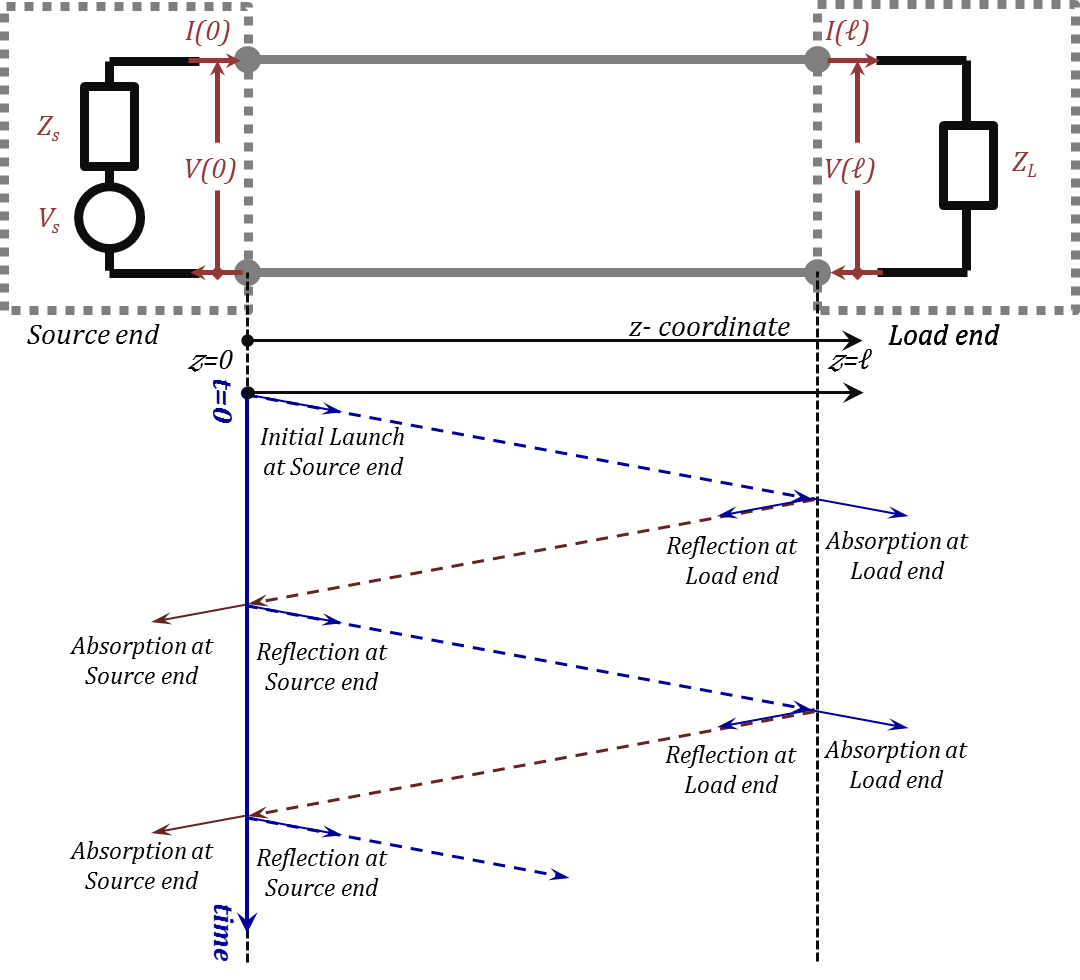
Figure 2.17

Using this bounce (reflection-transmission) diagram, let us now examine the physical meaning of the wave reflection and the corresponding reflection coefficient as defined in the frequency domain in Equation (2.50), $\text{ }\!\!\Gamma\!\!\text{ }\left( z \right)=\frac{{{V}^{-}}{{e}^{+~\gamma ~z}}}{{{V}^{+}}{{e}^{-~\gamma ~z}}}$. We claim that the ${{V}^{-}}{{e}^{+~\gamma ~z}}$ wave resulted from the reflections of the wave ${{V}^{+}}{{e}^{-~\gamma ~z}}$. Meanwhile, we do not see any discontinuities at a general location $z$ that can cause reflections at that location. So, where did the ${{V}^{-}}{{e}^{+~\gamma ~z}}$ come from? The answer lies in examining the transients build up before the steady state (harmonic) is reached.

In this regard, and based on the time-domain solution obtained earlier in Equation (2.29), a ${{v}^{+}}\left( z,t \right)$ wave, was initially launched at the sending end of the line. This wave traveled along the TL experiencing both attenuation and phase shift but no reflections until it met the first discontinuity at the load end. At the load "discontinuity", this wave suffered its first reflection triggering the backward traveling wave, ${{v}^{-}}\left( z,t \right)$. The reflected wave would then travel back to the source end experiencing only attenuation and phase change until it met the source end discontinuity. A source end reflection would then be in order and the bouncing back and forth continued. With each of these reflections, in general, some of the signal energy would be absorbed in the reflecting elements (the TL end termination impedances, ${{Z}_{L}}$ and ${{Z}_{s}})$.

At steady state, there will continue to be a multiple reflections at both line ends resulting in a series of $+z$ traveling waves and another series of $–z$ traveling waves. The sum of terms of each of these two series correspond to the two terms of the steady-state harmonic solution, ${{V}^{-}}{{e}^{+~\gamma ~z}}$ for the $+z$ series and ${{V}^{+}}{{e}^{-~\gamma ~z}}$ for the $–z$ series. (The proof of this statement will be carried out later in this chapter). sThe ratio between these two terms is what we defined as the reflection coefficient $\text{ }\!\!\Gamma\!\!\text{ }\left( z \right)$. So, as you can see, $\text{ }\!\!\Gamma\!\!\text{ }\left( z \right)$ does not physically exist as a localized phenomenon at the $z$ location of the line; rather, it is a result of the comprehensive performance of the whole setup as seen by the line at the $z$ location.

It is interesting to observe, that $\text{ }\!\!\Gamma\!\!\text{ }\left( z \right)$ has a localized physical meaning at $z=\ell $. At this location, and using Equation (2.49), ${{\text{ }\!\!\Gamma\!\!\text{ }}_{L}}=\text{ }\!\!\Gamma\!\!\text{ }\left( \ell \right)=~\frac{\left[ {{Z}_{L}}-{{Z}_{o}} \right]}{\left[ {{Z}_{L}}+{{Z}_{o}} \right]}$ which is determined by the discontinuity mismatch at that location and is totally independent of the rest of system.

Addendum A: Driving Point Impedance
TL Driving Point Impedance and Input Impedance:

It is obvious from the discussion above that the impedance relationships on a TL plays a dominant role in assessing its performance. For this reason, in the following section we will focus on developing some critical impedance relationships.

First, let us derive an expression for what we know as the "driving point impedance". This is the impedance seen by an observer at a given location on the line looking towards the load side, Figure 2.20.

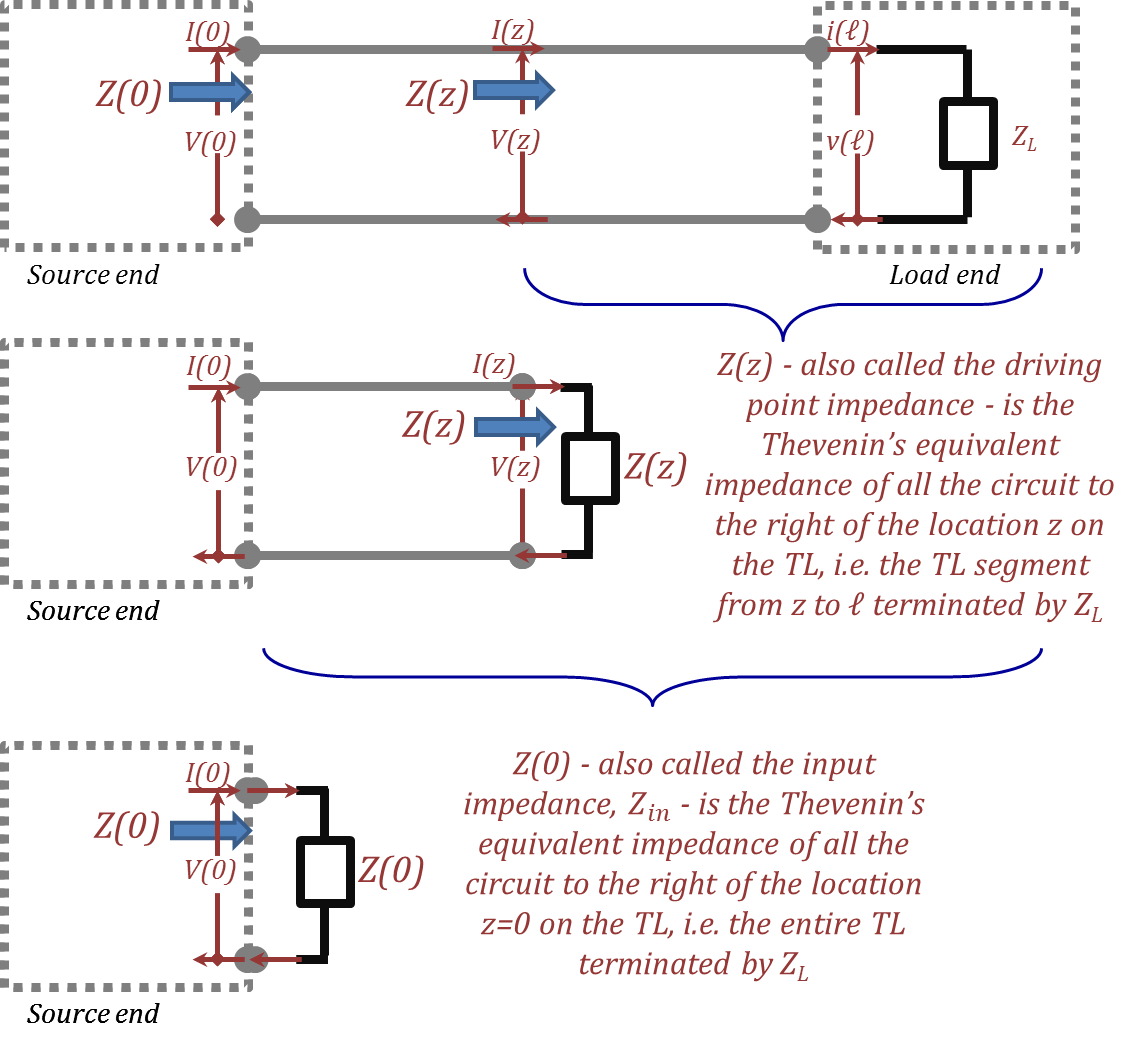
Figure 2.20

Using Equation (2.46) and (2.51) above,

$\text{Z}\left( z \right)=\frac{\text{V}\left( z \right)}{\text{I}\left( z \right)}=~{{\text{Z}}_{\text{o}}}\frac{\left[ 1+\text{ }\Gamma\text{ }\left( z \right) \right]}{\left[ 1-\text{ }\!\!\Gamma\!\!\text{ }\left( z \right) \right]}=~{{\text{Z}}_{\text{o}}}\frac{\left[ 1+\text{ }\Gamma\text{ }\left( \ell \right)~\cdot~ {{\text{e}}^{-2\text{ }\gamma\text{ d}}} \right]}{\left[ 1-\text{ }\Gamma\text{ }\left( \ell \right)~\cdot~ {{\text{e}}^{-2\text{ }\gamma\text{ d}}} \right]}=~{{\text{Z}}_{\text{o}}}\frac{\left[ 1+\frac{\left[ {{\text{Z}}_{\text{L}}}-{{\text{Z}}_{\text{o}}} \right]}{\left[ {{\text{Z}}_{\text{L}}}+{{\text{Z}}_{\text{o}}} \right]}~\cdot~ {{\text{e}}^{-2\text{ }\gamma\text{ d}}} \right]}{\left[ 1-\frac{\left[ {{\text{Z}}_{\text{L}}}-{{\text{Z}}_{\text{o}}} \right]}{\left[ {{\text{Z}}_{\text{L}}}+{{\text{Z}}_{\text{o}}} \right]}~\cdot~ {{\text{e}}^{-2\text{ }\gamma\text{ d}}} \right]}$

$\text{Z}\left( z \right)={{\text{Z}}_{\text{o}}}\frac{\left[ \left[ {{\text{Z}}_{\text{L}}}+{{\text{Z}}_{\text{o}}} \right]+\left[ {{\text{Z}}_{\text{L}}}-{{\text{Z}}_{\text{o}}} \right]~\cdot~ {{\text{e}}^{-2\text{ }\gamma\text{ d}}} \right]}{\left[ \left[ {{\text{Z}}_{\text{L}}}+{{\text{Z}}_{\text{o}}} \right]-\left[ {{\text{Z}}_{\text{L}}}-{{\text{Z}}_{\text{o}}} \right]~\cdot~ {{\text{e}}^{-2\text{ }\gamma\text{ d}}} \right]}={{\text{Z}}_{\text{o}}}\frac{\left[ \left[ {{\text{Z}}_{\text{L}}}+{{\text{Z}}_{\text{o}}} \right]~\cdot~ {{\text{e}}^{+\text{ }\gamma\text{ d}}}+\left[ {{\text{Z}}_{\text{L}}}-{{\text{Z}}_{\text{o}}} \right]~\cdot~ {{\text{e}}^{-\text{ }\gamma\text{ d}}} \right]}{\left[ \left[ {{\text{Z}}_{\text{L}}}+{{\text{Z}}_{\text{o}}} \right]~\cdot~ {{\text{e}}^{+\text{ }\gamma\text{ d}}}-\left[ {{\text{Z}}_{\text{L}}}-{{\text{Z}}_{\text{o}}} \right]~\cdot~ {{\text{e}}^{-\text{ }\gamma\text{ d}}} \right]}$

$\text{Z}\left( \text{d} \right)=\text{Z}\left( z \right)={{\text{Z}}_{\text{o}}}\frac{\left[ 2{{\text{Z}}_{\text{L}}}~\cdot~ \cosh \left( \text{ }\gamma\text{ d} \right)+2{{\text{Z}}_{\text{o}}}~\cdot~ \sinh \left( \text{ }\gamma\text{ d} \right) \right]}{\left[ 2{{\text{Z}}_{\text{L}}}~\cdot~ \sinh \left( \text{ }\gamma\text{ d} \right)+2{{\text{Z}}_{\text{o}}}~\cdot~ \cosh \left( \text{ }\gamma\text{ d} \right) \right]}={{\text{Z}}_{\text{o}}}\frac{\left[ {{\text{Z}}_{\text{L}}}+{{\text{Z}}_{\text{o}}}~\cdot~ \tanh \left( \text{ }\gamma\text{ d} \right) \right]}{\left[ {{\text{Z}}_{\text{o}}}+{{\text{Z}}_{\text{L}}}~\cdot~ \tanh \left( \text{ }\gamma\text{ d} \right) \right]}\tag{2.70}$

Hence,

${{\text{Z}}_{\text{in}}}=\text{Z}\left( z=0 \right)={{\text{Z}}_{\text{o}}}\frac{\left[ {{\text{Z}}_{\text{L}}}+{{\text{Z}}_{\text{o}}}~\cdot~ \tanh \left( \text{ }\gamma\text{ }\ell \right) \right]}{\left[ {{\text{Z}}_{\text{o}}}~+~{{\text{Z}}_{\text{L}}}~\cdot~ \tanh \left( \text{ }\gamma\text{ }\ell \right) \right]}\tag{2.71}$

To gain some insight into this expression, let take the lossless transmission line case where

$\text{ }\gamma\text{ }=j~\beta\text{ }~\text{ and }~\text{ }{{\text{Z}}_{\text{o}}}={{\text{R}}_{\text{o}}}$,

$\text{Z}\left( \text{d} \right)={{\text{R}}_{\text{o}}}\frac{\left[ {{\text{Z}}_{\text{L}}}+{{\text{R}}_{\text{o}}}~\cdot~ j~\text{tan}\left( \text{ }\beta\text{ d} \right) \right]}{\left[ {{\text{R}}_{\text{o}}}+{{\text{Z}}_{\text{L}}}~\cdot~ j~\text{tan}\left( \text{ }\beta\text{ d} \right) \right]}\tag{2.72}$

and since $\tan \left[ \beta \left( d\pm n\lambda /2 \right) \right]=\tan \left( \frac{2\pi d}{\lambda }\pm \pi \right)=\tan \left( 2\pi d/\lambda \right)=\tan \left( \beta d \right)$, then

$\text{Z}\left( \text{d}\pm \text{n }\lambda\text{ }/2 \right)=\text{Z}\left( \text{d} \right)$ or $\text{Z}\left( z\pm \text{n }\lambda\text{ }/2 \right)=\text{Z}\left( z \right)\tag{2.73}$

In other words, the impedance values repeat on a lossless line every half-wavelength while, as we recall, the voltage waves currents repeated every full wavelength.

Furthermore, since $\text{ }~\text{ tan}~\left[ \beta \left( d\pm n\lambda /4 \right) \right]=\tan \left( \frac{2\pi d}{\lambda }\pm \pi /2 \right)=-{{\left\{ \tan \left( \beta ~d \right) \right\}}^{-1}}$, then

$\text{Z}\left( d\pm n\lambda\text{ }/4 \right)={{\text{R}}_{\text{o}}}\frac{\left[ {{\text{Z}}_{\text{L}}}+{{\text{R}}_{\text{o}}}~\cdot~ {{\left\{ j\tan \left( \text{ }\beta\text{ d} \right) \right\}}^{-1}} \right]}{\left[ {{\text{R}}_{\text{o}}}+{{\text{Z}}_{\text{L}}}~\cdot~ {{\left\{ j~\text{ tan}\left( \text{ }\beta\text{ d} \right) \right\}}^{-1}} \right]}={{\text{R}}_{\text{o}}}\frac{\left[ {{\text{R}}_{\text{o}}}+{{\text{Z}}_{\text{L}}}~\cdot~ \text{j}~\text{tan}\left( \text{ }\beta\text{ d} \right) \right]}{\left[ {{\text{Z}}_{\text{L}}}+{{\text{R}}_{\text{o}}}~\cdot~ \text{j}~\text{tan}\left( \text{ }\beta\text{ d} \right) \right]}=\text{ }\text{ R}_{\text{o}}^{2}/~\text{Z}\left( \text{d} \right)\tag{2.74}$

Therefore, every quarter-wavelength the lossless TL driving point impedance inverses its nature.

Some Special Cases:

For a lossless line (almost true for low loss lines as well), we can summarize some features derived from Equation (2.72) in the Table (2.2):

Table 2.2

It is interesting to know that some of features cited in the above table have useful applications. One typical application is the use of a quarter-wavelength TL section to act as an impedance transformer (adapter).

${{\left. {{\text{Z}}_{\text{in}}} \right|}_{\text{ }\lambda\!\text{ }/4}}=\text{ }\!\!~\!\!\text{ R}_{\text{o}}^{2}/~{{\text{Z}}_{\text{L}}}\tag{2.75}$

Examples: A quarter-wavelength TL section terminated by a capacitor works as an inductor for use in high frequency devices. This is a highly preferred approach since wound coils do not offer the desired performance at radio and microwave frequencies. We find a similar approach in using a short-circuited quarter-wavelength TL section to act as an open circuit at high frequencies.

Another typical application is to use a quarter-wavelength TL section with the right value of ${{R}_{o}}$ to provide impedance matching between differing source and load resistive impedances.

$R_{o}^{2}={{\left. {{R}_{in}} \right|}_{\lambda /4}}\cdot {{R}_{L}}={{R}_{s}}\cdot {{R}_{L}}$, e.g. a $150~Ω$ quarter-wavelength TL can match a $75~Ω$ source to a $300~Ω$ load.

 

Video

1. Mention two TL cases for which a travelling signal experiences no reflections. 
2. When is a TL considered "matched"? 
3. What is the difference between a "standing wave" and a "propagating wave"? 
4. Under which condition is the wave on the TL free of any standing wave components? What is a common practical metric used to describe the ratio of the peak to the valley values of a standing wave? 
5. What is the distance between two peaks on a standing wave? 
6. What is the driving point input impedance for a lossless quarter wavelength long TL terminated by an open circuit? 

Return to Lesson

Return to Video

1. For a TL having the following parameters: $Z_{o}$ (characteristic impedance) $= 50~Ohm$, $Z_s=50~Ohm$ and $Z_L=75~Ohm$, $length=4\ cm$, and $f=20\ GHz$, calculate the reflection coefficient at the load, reflection coefficient at the source, driving point impedance at the source side and the $\text{SWR}~$? 
2. Using the same TL in 1 and using a voltage source of ${2~Volts}$, find the magnitude of each of the travelling wave components and the standing wave component in the TL voltage waves? 
3. Using the same TL in 1 with ${{Z}_{L}} = 0$ (short circuit), find the magnitude of the travelling wave and the standing wave components? Find the location of the first voltage peak away from the load. 
4. For a TL having the following parameters $Z_o=50~Ohm$, ${{Z}_{L}} = infinity$ (open circuit) and $f=3~GHz$, what should the length of the TL be for the driving point impedance at the source end equal to ${0~Ohm}$? 

Return to Lesson

Return to Video

1. A transmission line with characteristic impedance ${50~Ohm}$ and length $\ell \ $(distance from source to load) has a forward propagating wave ${{v}^{+}}(t,z)=2\ cos(\omega t-\beta z)$ and a reflected backward propagating wave ${{v}^{-}}(t,z)=0.5\ cos(\omega t+\beta z)$. Determine the value of the load impedance and the ${SWR}$ on the line. 
2. A lossless transmission line is terminated with a ${100~Ohm}$ load. If $SWR=2$, find the possible values of the characteristic impednace. 
3. For a transmission line with the following parameters: $Z_{o} = 50~Ohm$, $\ell = 0.3 $ λ and $Z_{L} = 20 -j10~Ohm$. Find the reflection coefficient at the load, at the source and find the driving point impedance at the source end. 
4. Consider the transmission line circuit with the following parameters: ${{V}_{s}}=2~Volts$, $Z_s=10~Ohm$, $Z_o=50~Ohm$, $\ell =0.3$ λ , and $Z_{L} = 75~Ohm$. Find the magnitude of each of the forward and backward travelling wave and the total voltage at the load end.
5. Consider a TL with the following per unit length model parameters: $R_{z} = 0.05~Ohm/m$, $L_z=0.5~uH/m$, $C_z=40~uF/m$, $G_z=1~mS/m$ terminated with an open circuit termination and operating at a frequency of ${5~GHz}$. Plot the driving point impedance (Magnitude and Phase – Real and Imaginary) at different point over a section of length ${30~mm}$.

Return to Lesson

Return to Video

Click here to download the Instructor Guide >>